◆公式◆
① 
②
②
【例】
【例】
【例題】
・ つのサイコロを
つのサイコロを 回投げる
回投げる
・ の倍数の目が
の倍数の目が 回出る確率を
回出る確率を とする。
とする。
・
・
①が最大となるときの
の値を求める
・の倍数の目が出る確率
・の倍数以外の目が出る確率
・サイコロを回投げて
の倍数が
回出るときの確率
※確率はいつ最大となるか?の公式より
※
公式 より
上記を以下の式に代入する
上記より
のとき(
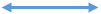
)

つまり
のとき(
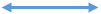
)
(不適)
のとき(
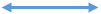
)

つまり
,
,
より
よって が最大ときの
は
② の 最大値を求めよ
①より のとき、つまり
が最大値